Using a gamma transformation followed by linear transforms in YUV color space to convert images for dark mode.
1. Solution
If you already know the problem, here's the solution:
<svg style="position:fixed; left:0; top:0; width:0; height:0">
<defs>
<filter id="invert-luminance"
color-interpolation-filters="linearRGB">
<feComponentTransfer>
<feFuncR type="gamma"
amplitude="1"
exponent="0.5"
offset="0.0"/>
<feFuncG type="gamma"
amplitude="1"
exponent="0.5"
offset="0.0"/>
<feFuncB type="gamma"
amplitude="1"
exponent="0.5"
offset="0.0"/>
<feFuncA type="gamma"
amplitude="1"
exponent="1"
offset="0.0"/>
</feComponentTransfer>
<feColorMatrix type="matrix" values="
1.000 -1.000 -1.000 0.000 1.000
-1.000 1.000 -1.000 0.000 1.000
-1.000 -1.000 1.000 0.000 1.000
0.000 0.000 0.000 1.000 0.000
"/>
</filter>
</defs>
</svg>Stick that at the top of your HTML and then use style="filter:url(#invert-luminance)" on the images you want to invert.
2. Problem
With dark mode on mobile devices and the associated CSS prefers-color-scheme: dark, there is a need to re-color line art - diagrams, charts, etc. - so they blend in on the page. Any drawing made to look good against a white background must be re-colored to look good against a black background.
Manually doing this is a hassle, so many web designers reach for some way to do this automatically in the browser. Equally many end up grabbing the combination of filter: invert() and filter: hue-rotate(180deg), only to drop it just as quickly. The combination works in theory: the invert() turns white into black and vice versa and also flips all colors around, but the hue-rotate(180deg) should restore the colors. This should leave us with what we want - the black-and-white line art has maximum contrast, and the colors are the same.
But since a hue rotation isn't a linear operator the web browser cheats and uses an approximation which results in the colors ending up much darker than you'd expect:

The goal was to produce a CSS-compatible color transform that can produce acceptable results for most common cases.
3. Derivation
First, it's necessary to note that a perfect hue rotation cannot be done with linear transformations of RGB colors. What we're looking for is an approximation that gives good results on the typical inputs - line art made to be displayed against a white background.
White should map to black, and black to white
Hues should be preserved
We start by following busybee's Affine HSV color manipulation[a] and transform RGB into a luminance+chrominance color space. What this basically means is that one channel will be the weighted average of the RGB channels and the other two will be the difference between the luminance and two of the RGB channels. In YUV, the green channel has the highest weight in the luminance channel Y, and the U and V channels are the blue-difference (B-Y) and red-difference (R-Y), respectively. Other options are YIQ and YCbCr - they're all the same, with some difference in which components are selected and the relative weights.
W_r = 0.299
W_g = 1.0 - W_r - W_b = 0.587
W_b = 0.114
U_max = 0.436
V_max = 0.615
Y = W_r r + W_g g + W_b b
U = U_max/(1-W_b) (b - Y)
V = V_max/(1-W_r) (r - Y)
U_s = U_max/(1-W_b)
V_s = V_max/(1-W_r)
U = - U_s W_r r - U_s W_g g + U_s (1 - W_b) b
V = + V_s (1 - W_r) r - V_s W_g g - V_s W_b b
M_("lc") = [[W_r, W_g, W_b, 0], [- U_s W_r , - U_s W_g , + U_s (1 - W_b), 0], [+ V_s (1 - W_r) , - V_s W_g , - V_s W_b, 0], [0,0,0,1]]
Once in YUV space, a hue rotation can be done by rotating the UV vector. For a 180 degree rotation the U and V vectors are simply negated:
M_("hue") = [[1, 0, 0, 0], [0, -1, 0, 0], [0, 0, -1, 0], [0, 0, 0, 1]]
An inversion is equally simple - we just negate the matrix and remember to augment the final filter matrix with the correct constant to bring the output range [-1 0] back to [0 1]:
M_("inv") = [[-1, 0, 0, 0], [0, -1, 0, 0], [0, 0, -1, 0], [0, 0, 0, 1]]
Finally, the RGB-to-YUV transform matrix is invertible, so we use it to return to RGB color space.
M_("rgb") = M_("lc")^-1
Since all steps are linear we concatenate the matrices, saving us the trouble of worrying about out-of-range values, rounding errors, etc.:
M_("transform") = M_("rgb")M_("hue")M_("inv")M_("lc")
And we don't forget to augment the matrix at the end:
M_("filter") = M_("transform")| ((1),(1),(1),(0))
Done. Let's take it for a spin:


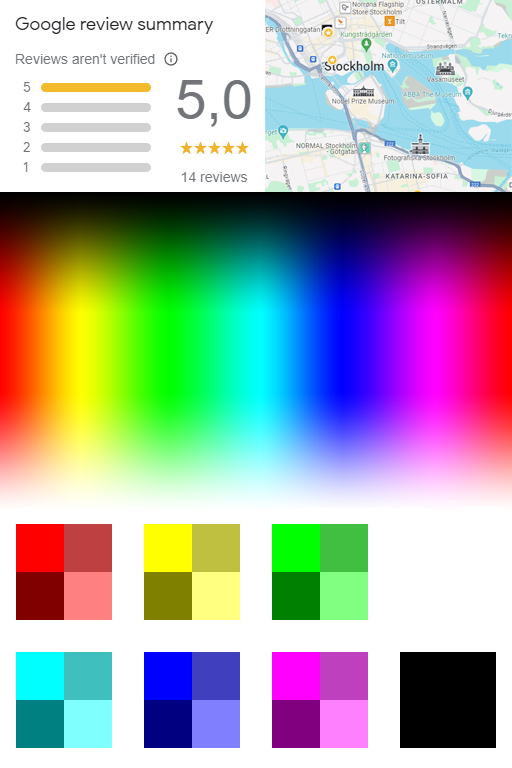
Looks OK on the Google Maps review sample, but the saturated colors look off:
The green is too dark
The red is too bright
The blue is far too bright
Everything is too desaturated
We'll take these in two steps. First, the brightness problem. This is caused by the relative weights used to compute Y. Since the weight for green is the greatest, a pure-green color is seen as very bright and is inverted to something dark. A pure-blue color is seen as very dark by the transform and is therefore inverted to a very bright, almost white, blue.
We'll just eyeball some new weights: 1/3 for each.


Looking better, but the colors are still very desaturated. Fortunately we can boost the saturation in the transform by scaling the UV vector by a constant. Again, let's just eyeball it (remember, there is no "right answer" - hue rotations are not linear so the problem can't be solved perfectly) and double the vector:
M_("sat") = [[1, 0, 0, 0], [0, S, 0, 0], [0, 0, S, 0], [0, 0, 0, 1]]
= [[1, 0, 0, 0], [0, 2, 0, 0], [0, 0, 2, 0], [0, 0, 0, 1]]
We'll just stick that between M_(rgb) and M_(hue):


Better, but the colors are still washed out. A bit of thinking reveals that any color in YUV space with a Y > 0.5 will be desaturated, and that saturated colors only exist below Y = 0.5. In short, our saturated color gets inverted into the upper half of Y. We can't just darken the input linearly, as we must still map black to white and vice versa, but we can do something else: a gamma filter.
Adding a gamma = 0.5 filter to the input brightens it a lot while still leaving black and white unchanged. When the color is then inverted it should land in the lower half of the range:


Finally, the U_(max) and V_(max) can be anything since we don't have to produce compliant YUV values, so we'll just set those to 1.0 to clean things up. And this is where I left it.
4. Try It
| Wr | |
| Wg | |
| Wb | |
| Umax | |
| Vmax | |
| Saturation | |
| Gamma |

