Parallel For and ForEach
The Single-Instruction-Multiple-Data, or SIMD, type of multiprocessing is a staple of multicore programming. In such a process, the same instruction stream is used for a number of data streams; think of it as a "for all these data items, do this to each one of them". Often it is realized by a parallel for-loop. Java, however, has no parallel for primitive, so we'll build one on top of the work set abstraction.
1. Dividing the Work
The key to dividing work is to split it in work units that are large enough that the switching overhead is very small compared to the total execution cost, yet small enough that all available CPU cores are utilized and that difference in execution cost among the work units can be compensated for by moving units to other cores. Let's go through these three requirements one by one:
-
Large enough to avoid switching costs: Let's say that we are to perform a very fast operation 1000 times. If the cost of the operation is 1, and the overhead inherent in every work unit is 10, we get the following total cost, depending on the number of operations in each work unit:
Total execution cost for different work unit sizes Ops/Unit Units Cost 1 1000 11000 10 100 2000 100 10 1100 1000 1 1010 -
Small emough to keep the cores busy: As we can see in the table, the more operations we pack into each work unit, the less the total cost becomes. The lowest total cost is when we put all the fast operations in a single work unit. But this hides an important fact: The total cost isn't equal to the total runtime! Since each work unit executes concurrently with all others up to the number of cores, the total execution time changes in a way that is much more attractive. Assuming a ten-core system, we get:
Total execution cost and time for different work unit sizes Ops/Unit Units Cost Time 1 1000 11000 1100 10 100 2000 200 100 10 1100 110 1000 1 1010 1010 That looks a lot better! All cases with more than ten work units keep the cores busy, since we can give each core at least one work unit. The case with a single work unit is now the next to worst-performing, since it results in nine idle cores. We get the shortest execution time for ten work units of 100 operations each - precisely when the number of work units equal the number of cores. For all cases when the switching cost is negligible compared to the cost of the work unit, this is the most optimal.
-
Small enough to compensate for differences: In the examples above we have assumed that the work that needs to be done is of a constant, measurable cost. In most cases, this is not known in advance, and the cost can vary wildly. First, let's get rid of the overhead cost; to avoid the typical large numbers, we'll just assume a switching cost of zero. Let's say that we have two types of operations: Fast and slow. The fast operations have a cost of 1, as before. The slow operations have a cost of 50, but are comparatively rare - only one in a thousand operations. For our example, then, we can assume that we have 999 fast operations and one slow. If we split the operations into ten units and submit them, nine cores will get 100 fast operations - a total execution cost of 100 - and one poor core will get 99 fast operations and one slow - a total execution cost of 149, almost 50% higher.
However, if we split the work into 50 units of 20 operations each, then, provided that the cores work off a common queue, nine cores will process five work units each for a total execution cost of 100. The tenth core will (we assume for simplicity) start with the slow operation (50) followed by 19 fast operations (19) and reach an execution cost of 69 after the first work unit. When it has done a little more than one and a half work units more, it will also have reached a total execution cost of 100. At this point the tenth core has claimed three work units, meaning that a total of 48 work units are either completed or about to be completed. But the two units left can now be grabbed by any two of the first nine cores, and be completed in 20 units of execution cost. When all units have been processed, the cores that have done the most work will have a total execution cost of 120. This is still more than the ideal case where each core ends with an execution cost of 104.9, but where the previous example was 42% above ideal, this is only 14% above.
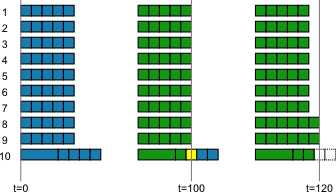
The state of the cores and work units The state of the cores and work units are shown during three points in time in the process described above. To the left, just before starting, in the middle after nine out of ten cores finish, and to the right when all cores have finished.
As we keep splitting the work even finer this overhead is reduced, but sooner or later we can no longer disregard the switching cost and performance starts to suffer again.
The rule of thumb I have is: Split the work into work units that are just big enough to make the switching cost negligible, but never in more than four times the maximum number of cores they may run on.
Now that we can divide the work, it's time to look at the code.
2. Integer Loop
The integer loop is parameterized by two numbers: The lowest and one-beyond the highest integer. The canonical form is for (int i = low; i < high; ++i) { ... }, and even if high is one-past the highest value i will ever have in the loop, the idiom is so strong that designing the interface with that in mind makes sense.
We also need an interface for the client:
public interface ParallelFor<R> {
/**
* Execute for (int i = a; i < b; ++i)
*/
public R call (int a, int b) throws Exception;
}The implementation is then:
public void parallelFor (
int a,
int b,
int minWorkUnitSize,
final ParallelFor<Result> pfor
) throws Exception {
int delta = b - a;
int step = delta / (getNumCores () * 4);
if (step < minWorkUnitSize) {
step = minWorkUnitSize;
}
int i = a;
while (i < b) {
int start = i;
int end = i + step;
if (end > b) {
end = b;
}
final int fs = start;
final int fe = end;
execute (
new Callable<Result> () {
public Result call () throws Exception {
return pfor.call (fs, fe);
}
}
);
i = end;
}
}3. Iterator
In the iterator case we can't split the work into work units, as that would require[1] iterating over the whole collection and creating N separate sub-collections that can then be fed to N work units. Instead, to iterate over a Collection, we will first obtain an Iterator for that collection. From that iterator we will then feed N buffered iterators that are used by the same number of work units:
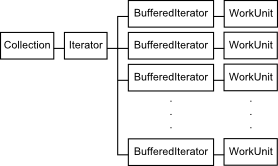
The buffered iterator is simply a java. that has a prefetch buffer. Because iterators aren't thread safe by default, the buffered iterators must synchronize on the collection iterator when retrieving items. The prefetch helps amortize the synchronization overhead.
public interface ParallelForEach<T,R> {
/**
* Execute for (T t : iter)
*/
public R call (Iterable<T> iter) throws Exception;
} We will simply submit as many work units as there are cores, and let them use a buffered iterator linked to an iterator over the collection. If fewer cores are available than the number installed, the superfluous work units will receive empty iter iterables.
public <T> void parallelForEach (
final Iterator<T> iter,
int size,
int maxPrefetch,
final ParallelForEach<T,Result> piter
) throws Exception {
int numWorkUnits = getNumCores ();
if (numWorkUnits > size) {
numWorkUnits = size;
}
int chunkSize = (int) Math.ceil (((double) size) / numWorkUnits);
final int prefetch = chunkSize < maxPrefetch
? chunkSize : maxPrefetch;
for (int i = 0; i < numWorkUnits; ++i) {
execute (
new Callable<Result> () {
public Result call () throws Exception {
return piter.call (
BufferedIterator.<T>asIterable (iter, prefetch));
}
}
);
}
}